Coloration de graphe - exercices¶
Exercice 1¶
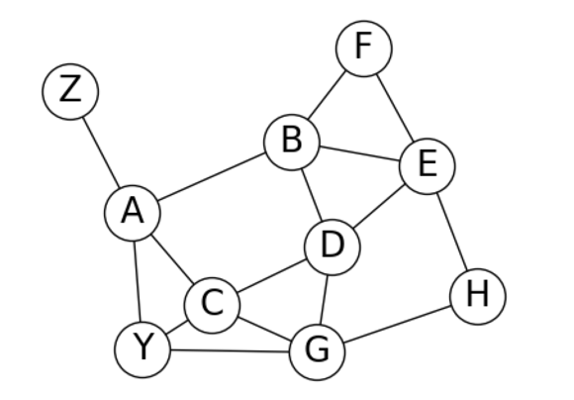
Colorer les sommets de ce graphe en utilisant l’algorithme de Welsh-Powell.
Exercice 2¶
Une entreprise qui fabrique six sortes de produits chimiques différents (notés P1, P2, P3, P4, P5, P6) doit en assurer le transport par train. Ces produits sont en petite quantité, mais ne peuvent être tous placés dans le même wagon pour des raisons de sécurité (le contact entre certains de ces produits peut provoquer des réactions explosives). Plus précisément :
P1 ne peut être transporté avec P2, P3, ou P4.
P2 ne peut être transporté avec P1, P3 ou P5.
P3 ne peut être transporté avec P1, P2 ou P4.
P5 ne peut être transporté avec P2 ou P6.
Combien de wagons au mininum sont-ils nécessaires au transport des six produits ? Pour répondre à cette question, construire le graphe représentant la situation et appliquer l’algorithme de Welch-Powell, chaque couleur représentera un wagon différent.
Exercice 3¶
A, B, C, D, E, F et G désignent 7 espèces animales ne pouvant pas partager le même enclos dans un zoo. Dans le tableau ci-dessous, une croix signifie que les espèces animales ne peuvent cohabiter dans un même enclos :
A |
B |
C |
D |
E |
F |
G |
|
|---|---|---|---|---|---|---|---|
A |
x |
x |
x |
||||
B |
x |
x |
x |
x |
|||
C |
x |
x |
|||||
D |
x |
x |
x |
x |
|||
E |
x |
x |
|||||
F |
x |
x |
|||||
G |
x |
x |
x |
x |
x |
Construire le graphe représentant cette situation.
Déterminer le nombre minimum d’enclos nécessaire et proposer une répartition des espèces qui respecte les contraintes données.
Exercice 4¶
Appliquer l’algorithme de Welsh-Powell sur la matrice d’adjacence des cantons suisses.
Canton |
Nombre de voisins |
Voisins |
|---|---|---|
BE |
10 |
SO, JU, NE, FR, VD, VS, OW, NW, LU, AG |
UR |
7 |
SZ, NW, OW, VS, TI, GR, GL |
SG |
7 |
TG, ZH, SZ, GL, GR, AI, AR |
SZ |
7 |
ZH, ZG, LU, NW, UR, GL, SG |
ZH |
6 |
AG, ZG, SZ, SG, TG, SH |
AG |
6 |
BL, SO, BE, LU, ZG, ZH |
LU |
6 |
AG, BE, OW, NW, SZ, ZG |
VD |
5 |
GE, VS, BE, FR, NE |
NW |
5 |
LU, OW, UR, BE, SZ |
ZG |
4 |
AG, LU, SZ, ZH |
BL |
4 |
BS, JU, SO, AG |
OW |
4 |
BE, LU, NW, UR |
JU |
4 |
NE, BE, SO, BL |
SO |
4 |
BL, JU, BE, AG |
GL |
4 |
SG, SZ, UR, GR |
VS |
4 |
VD, BE, UR, TI |
GR |
4 |
SG, GL, UR, TI |
NE |
4 |
JU, BE, FR, VD |
FR |
3 |
NE, VD, BE |
TG |
3 |
SH, ZH, SG |
TI |
3 |
VS, UR, GR |
SH |
2 |
ZH, TG |
AR |
2 |
SG, AI |
AI |
2 |
SG, AR |
BS |
1 |
BL |
GE |
1 |
VD |
Exercice 5¶
Considérons un ensemble de tâches (de A à M) ayant chacune une heure de début et une heure de fin bien précises. Supposons qu’on demande à des personnes d’effectuer ces tâches, mais qu’aucune personne ne puisse effectuer deux tâches à la fois.
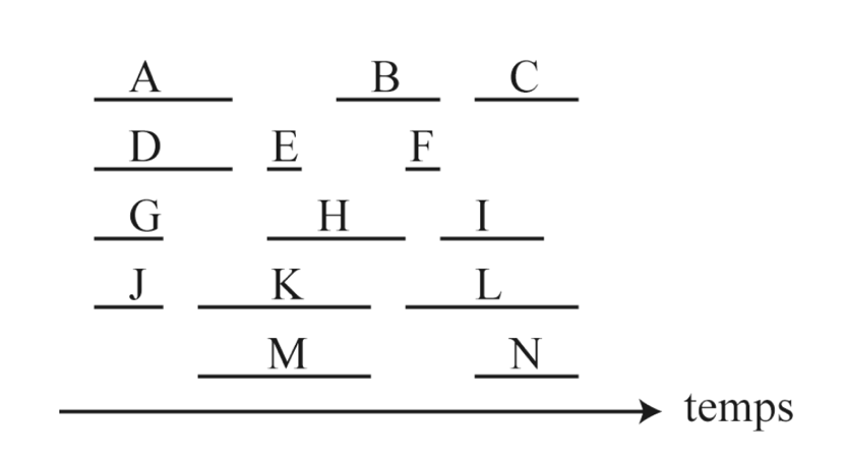
Horaire des tâches¶
Utiliser l’algorithme de Welch-Powell pour trouver le nombre minimum de personnes nécessaire pour effectuer toutes ces tâches et les répartir entre les différentes personnes.